AlphaGo_Zero

人工知能の長年の目標は、困難な分野において、全くの白紙の状態から超人的な能力を習得するアルゴリズムです。最近、AlphaGoは囲碁の世界チャンピオンを破った最初のプログラムとなりました。AlphaGoの木探索は、ディープニューラルネットワークを用いて局面を評価し、手を選択します。これらのニューラルネットワークは、人間の専門家の手からの教師あり学習と、自己対戦からの強化学習によって学習されました。本稿では、人間のデータ、ガイダンス、ゲームルール以外のドメイン知識を必要とせず、強化学習のみに基づくアルゴリズムを紹介します。AlphaGoは自らを教師とします。ニューラルネットワークは、AlphaGo自身の手の選択と、AlphaGoの対局の勝者を予測するように学習されます。このニューラルネットワークは木探索の強度を向上させ、次の反復におけるより質の高い手の選択と、より強力な自己対戦を実現します。白紙の状態からスタートした私たちの新しいプログラムAlphaGo Zeroは、超人的なパフォーマンスを達成し、以前に公開され、チャンピオンを破ったAlphaGoに100対0で勝利しました。

(はじめに)

人工知能の開発は、人間の専門家の意思決定を再現するように学習させる教師あり学習システムを用いることで大きく進歩してきました^1–4。しかし、専門家のデータセットは高価であったり、信頼性が低い場合が多く、あるいは入手困難な場合もあります。たとえ信頼できるデータセットが利用可能であったとしても、このように学習させたシステムの性能には限界がある可能性があります⁵。これに対し、強化学習システムは自身の経験から学習するため、原理的には人間の能力を超え、人間の専門知識が不足している領域でも動作することができます。近年、強化学習によって学習させたディープニューラルネットワークを用いることで、この目標に向けた急速な進歩が見られます。これらのシステムは、Atari^6,7などのコンピュータゲームや3D仮想環境^8–10において、人間を上回る性能を発揮しています。しかし、囲碁のように人間の知性にとって最も困難な領域では、広大な探索空間における正確かつ高度な先読みが求められます。囲碁は人工知能¹¹にとって大きな課題と広く考えられています。完全に汎用的な手法は、これまでこれらの領域において人間レベルのパフォーマンスを達成していません。

AlphaGoは、囲碁において超人的なパフォーマンスを達成した最初のプログラムでした。公開されたバージョン¹²（AlphaGo Fanと名付けました）は、2015年10月にヨーロッパチャンピオンの樊慧を破りました。AlphaGo Fanは、2つのディープニューラルネットワーク、すなわち手の確率を出力するポリシーネットワークと、局面の評価を出力するバリューネットワークを使用していました。ポリシーネットワークは、最初に教師あり学習によって人間の専門家の手を正確に予測するように学習され、その後、ポリシー勾配強化学習によって改良されました。バリューネットワークは、ポリシーネットワークが自身と対戦したゲームの勝者を予測するように学習されました。学習後、これらのネットワークはモンテカルロ木探索（MCTS: Monte Carlo Tree Search）^13-15と組み合わせられ、先読み探索が行われました。ポリシーネットワークは、高確率の手に探索を絞り込み、バリューネットワーク（高速ロールアウトポリシーを使用したモンテカルロロールアウトと組み合わせて）は、木内の局面を評価しました。その後のバージョンであるAlphaGo Leeも同様のアプローチ（「方法」参照）を採用し、2016年3月に18回の国際タイトル獲得者であるイ・セドルを破りました。

我々のプログラムAlphaGo Zeroは、AlphaGo FanやAlphaGo Lee¹²とはいくつかの重要な点で異なります。第一に、教師や人間のデータを用いることなく、ランダムプレイから開始する自己対戦強化学習のみで学習されます。第二に、入力特徴として盤上の白と黒の石のみを使用します。第三に、方策ネットワークと価値ネットワークを別々に使用せず、単一のニューラルネットワークを使用します。最後に、モンテカルロロールアウトを一切行わず、この単一のニューラルネットワークに基づくより単純な木探索を用いて局面を評価し、手番をサンプルします。これらの結果を達成するために、我々は学習ループ内に先読み探索を組み込んだ新しい強化学習アルゴリズムを導入し、迅速な改善と正確で安定した学習を実現しました。探索アルゴリズム、学習手順、ネットワークアーキテクチャにおけるその他の技術的な違いについては、「方法」で説明します。

AlphaGo Zero における強化学習

私たちの新しい手法では、パラメータ \(θ\) を持つディープニューラルネットワーク \(f_θ\) を使用します。このニューラルネットワークは、局面とその履歴の生の盤面表現 \(s\) を入力として受け取り、手確率と値 \((\mathbf p, v) = f_θ(s)\) の両方を出力します。手確率のベクトル \(\mathbf p\) は、各手 \(a\)（パスを含む）を選択する確率を表します \(p_a = Pr(a|s)\)。値 \(v\) はスカラー評価であり、局面 \(s\) から現在のプレイヤーが勝利する確率を推定します。このニューラルネットワークは、ポリシーネットワークとバリューネットワーク¹² の両方の役割を単一のアーキテクチャに統合します。ニューラルネットワークは、バッチ正規化¹⁸とReLU¹⁹を備えた畳み込み層^16,17の多数の残差ブロック⁴で構成されています（方法を参照）。

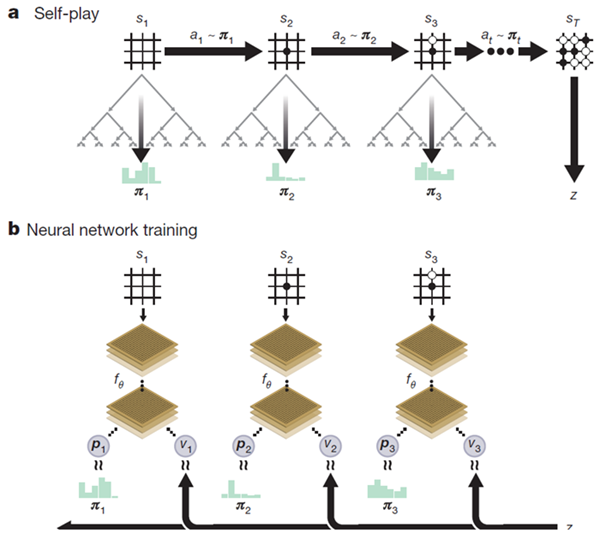
AlphaGo Zeroのニューラルネットワークは、新たな強化学習アルゴリズムによって自己対戦のゲームから学習される。各局面 \(s\) において、ニューラルネットワーク \(f_θ\) の誘導によりMCTS探索が実行される。MCTS探索は、各手を指す確率 \(\mathbf π\) を出力する。これらの探索確率は通常、ニューラルネットワーク \(f_θ(s)\) の生の手確率 \(\mathbf p\) よりもはるかに強い手を選択する。したがって、MCTSは強力な方策改善演算子と見なすことができる^20,21。探索を伴う自己対戦（改良されたMCTSベースの方策を用いて各手を選択し、ゲームの勝者zを値のサンプルとして使用する）は、強力な方策評価演算子と見なすことができる。私たちの強化学習アルゴリズムの主なアイデアは、これらの探索演算子を方策反復手順^22,23において繰り返し用いることです。ニューラルネットワークのパラメータは、移動確率と値 \((\mathbf p,v) = f_θ(s)\) が、改善された探索確率と自己対戦の勝者 \((\mathbf π, z)\) に近づくように更新されます。これらの新しいパラメータは、次の自己対戦の反復で使用され、探索をさらに強化します。図1は、自己対戦のトレーニングパイプラインを示しています。

図1 | AlphaGo Zeroにおける自己対戦強化学習。a プログラムは自身と対戦し、対局\(s_1, ..., s_T\)を行う。各局面\(s_t\)において、最新のニューラルネットワーク\(f_θ\)を用いてMCTS \(α_θ\)が実行される（図2参照）。手はMCTSによって計算された探索確率、\(a_t\sim π_t\)に従って選択される。最終局面\(s_T\)はゲームのルールに従って得点され、ゲームの勝者\(z\)が算出される。b AlphaGo Zeroにおけるニューラルネットワークの学習。ニューラルネットワークは、生の盤面の位置 \(s_t\) を入力として受け取り、パラメータ \(θ\) を持つ多数の畳み込み層にそれを通し、動きの確率分布を表すベクトル \(\mathbf p_t\) と、現在のプレイヤーが位置 \(s_t\) で勝つ確率を表すスカラー値 \(v_t\) の両方を出力します。ニューラルネットワークのパラメータ \(θ\) は、方策ベクトル \(\mathbf p_t\) と探索確率 \(\mathbf π_t\) の類似度を最大化し、予測される勝者 \(v_t\) とゲームの勝者 \(z\) の間の誤差を最小化するように更新されます (式 (1) を参照)。新しいパラメータは、a と同様に、次の自己対戦の反復で使用されます。

MCTSはニューラルネットワーク\(f_θ\)を用いてシミュレーションを誘導する（図2参照）。探索木の各辺\((s, a)\)には、事前確率\(P(s, a)\)、訪問回数\(N(s, a)\)、行動値\(Q(s, a)\)が格納される。各シミュレーションはルート状態から開始し、上側信頼限界\(Q(s, a) + U(s, a)\)（ただし\(U(s, a) ∝ P(s, a) /(1 + N(s, a))\)（参考文献12、24）を最大化する動きを、リーフノードs′に到達するまで反復的に選択する。この葉の位置は、ネットワークによって一度だけ拡張および評価され、事前確率と評価の両方が生成されます。\((P(s^\prime, ·),V(s^\prime)) = f_θ(s^\prime)\)。シミュレーションで通過する各エッジ\((s, a)\)は、訪問回数\(N(s, a)\)を増分するように更新され、アクション値はこれらのシミュレーション全体の平均評価に更新されます。\(Q(s,a)= 1/N(s,a)\sum_{s^\prime|s,a\to s^\prime}V(s^\prime)\)。ここで、\(s, a→ s^\prime\)は、シミュレーションが位置 \(s\) から移動 \(a\) を実行した後、最終的に \(s^\prime\) に到達したことを示します。

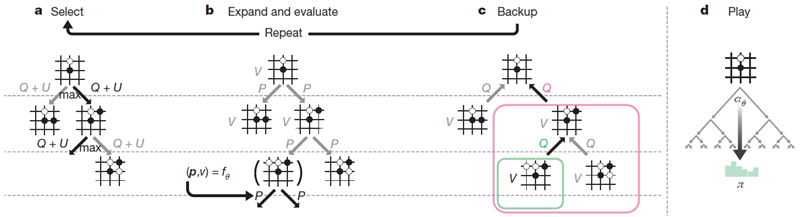
図2 | AlphaGo ZeroにおけるMCTS。a 各シミュレーションは、最大のアクション値 \(Q\) と、そのエッジの保存された事前確率 \(P\) と訪問回数 \(N\)（走査ごとに増加）に依存する信頼上限 \(U\) を持つエッジを選択して、ツリーを走査します。bリーフノードが展開され、関連する位置 \(s\) がニューラルネットワーク \((P(s, ·),V(s)) = f_θ(s)\) によって評価されます。\(P\) 値のベクトルは \(s\) からの出力エッジに格納されます。cアクション値 \(Q\) は、そのアクションの下位のサブツリー内のすべての評価 \(V\) の平均を追跡するように更新されます。 d 探索が完了すると、\(N^{1/τ}\) に比例する探索確率 \(π\) が返されます。ここで、\(N\) はルート状態からの各移動の訪問回数、\(τ\) は温度を制御するパラメーターです。

MCTSは、ニューラルネットワークパラメータ \(θ\) とルートポジション \(s\) が与えられたときに、各手の指数化された訪問回数 \(π_a ∝ N(s, a)^{1/τ}\) に比例する、プレイすべき手を推奨する探索確率のベクトル \(\mathbf π = α_θ(s)\) を計算する自己プレイアルゴリズムと見なすことができます。ここで、\(τ\) は温度パラメータです。

ニューラルネットワークは、各手に対してMCTSを用いてプレイするセルフプレイ強化学習アルゴリズムによって学習される。まず、ニューラルネットワークはランダムな重み \(θ_0\) に初期化される。その後の各反復 \(i ≥ 1\) において、セルフプレイのゲームが生成される（図1a）。各タイムステップ \(t\) において、ニューラルネットワークの前回の反復 \(f_{θ_{l-1}}\) を用いてMCTS探索 \(\mathbf π_t =α_{θ_{l-1}}(s_t)\) が実行され、探索確率 \(\mathbf π_t\) をサンプリングすることで手がプレイされる。両プレイヤーがパスするか、探索値が投了閾値を下回るか、ゲームが最大長を超えると、ステップ \(T\) でゲームは終了する。その後、ゲームはスコアリングされ、最終報酬 \(r_T ∈ \{-1,+1\}\) が与えられる（詳細は「方法」を参照）。各タイムステップ t のデータは \((s_t, \mathbf π_t, z_t)\) として保存されます。ここで、zt = ± rT は、ステップ t における現在のプレイヤーの視点からのゲームの勝者です。並行して (図 1b)、新しいネットワークパラメータ \(θ_i\) が、最後のセルフプレイの反復の全タイムステップから均一にサンプリングされたデータ \((s, \mathbf π, z)\) から学習されます。ニューラルネットワーク \((\mathbf p, v)= f_{θ_i} (s)\) は、予測値 \(v\) とセルフプレイの勝者 \(z\) の間の誤差を最小化し、ニューラルネットワークの移動確率 \(\mathbf p\) と検索確率 \(\mathbf π\) の類似性を最大化するように調整されます。具体的には、パラメータθは、平均二乗誤差とクロスエントロピー損失をそれぞれ合計する損失関数lの勾配降下法によって調整されます。 \[ (\mathbf p,v)=f_\theta(s)　and　l=(z-v)^2-\boldsymbol{\pi}^T \log \mathbf p+c||\theta||^2 \tag{1} \] ここで、\(c\) は L2 重み正則化のレベルを制御するパラメータです（過学習を防ぐため）。

AlphaGo Zero の学習に関する実証的分析

強化学習パイプラインを適用し、プログラム AlphaGo Zero を学習しました。学習は完全にランダムな動作から始まり、約 3 日間、人間の介入なしに継続されました。

訓練期間中、各MCTSについて1,600回のシミュレーションを用いて490万局の自己対局が生成されました。これは、1手あたり約0.4秒の思考時間に対応します。パラメータは、2,048局面からなる70万回のミニバッチから更新されました。ニューラルネットワークには20個の残差ブロックが含まれていました（詳細は「方法」を参照）。

図3aは、自己対戦強化学習中のAlphaGo Zeroの性能を、訓練時間の関数としてEloスケール25上で示しています。学習は訓練全体を通してスムーズに進行し、先行研究26-28で示唆されている振動や壊滅的な忘却は発生しませんでした。驚くべきことに、AlphaGo Zeroはわずか36時間でAlphaGo Leeを上回りました。比較すると、AlphaGo Leeは数か月かけて訓練されました。72時間後、ソウルでのマンマシン対局で使用されたのと同じ2時間の時間制限と対局条件下で、イ・セドルを破ったAlphaGo Leeの正確なバージョンとAlphaGo Zeroを評価しました（方法を参照）。AlphaGo Zeroは4つのテンソル処理ユニット（TPU）29を搭載した単一のマシンを使用していましたが、AlphaGo Leeは複数のマシンに分散され、48個のTPUを使用していました。 AlphaGo ZeroはAlphaGo Leeを100対0で破りました（拡張データ図1および補足情報を参照）。

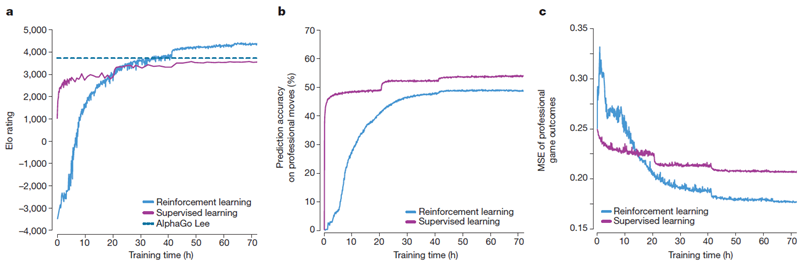
図3 | AlphaGo Zero の実証的評価。a セルフプレイ強化学習の性能。このグラフは、AlphaGo Zero における強化学習の各反復 i における各 MCTS プレイヤー αθi の性能を示しています。Elo レーティングは、異なるプレイヤー間の評価ゲームから計算され、1手あたり0.4秒の思考時間を使用しました（「方法」を参照）。比較のために、KGS データセットを用いて人間のデータから教師あり学習によって訓練された同様のプレイヤーも示されています。b 人間のプロの指し手の予測精度。このグラフは、GoKifu データセットから人間のプロの指し手を予測する際の、セルフプレイ \(i\) の各反復におけるニューラルネットワーク \(f_{θ_i}\) の精度を示しています。この精度は、ニューラルネットワークが人間の指し手に最も高い確率を割り当てた局面の割合を測定します。教師あり学習によって訓練されたニューラルネットワークの精度も示されています。c 人間のプロの対局結果の平均二乗誤差（MSE）。このグラフは、GoKifuデータセットから人間のプロの対局結果を予測する際の、ニューラルネットワーク\(f_{θ_i}\)の自己対局\(i\)の各反復におけるMSEを示しています。MSEは、実際の結果\(z ∈ \{-1, +1\}\)とニューラルネットワーク値\(v\)との間の値であり、\(\frac{1}{4}\)倍して0～1の範囲にスケーリングされています。教師あり学習によって訓練されたニューラルネットワークのMSEも示されています。

人間のデータからの学習と比較した自己対戦強化学習のメリットを評価するために、KGSサーバーデータセットで専門家の手を予測するように、同じアーキテクチャを使用した2つ目のニューラルネットワークを訓練しました。このネットワークは、以前の研究12,30–33と比較して最先端の予測精度を達成しました（現在の結果と以前の結果については、それぞれ拡張データ表1と表2を参照）。教師あり学習はより良い初期パフォーマンスを達成し、人間のプロの手を予測する能力も優れていました（図3）。注目すべきは、教師あり学習の方が高い手予測精度を達成したにもかかわらず、自己学習したプレイヤーは全体的にはるかに優れたパフォーマンスを発揮し、訓練開始から24時間以内に人間が訓練したプレイヤーに勝利したことです。これは、AlphaGo Zeroが人間のプレイとは質的に異なる戦略を学習している可能性があることを示唆しています。

アーキテクチャとアルゴリズムの寄与を分離するため、AlphaGo Zeroのニューラルネットワークアーキテクチャの性能を、AlphaGo Leeで使用されていた以前のニューラルネットワークアーキテクチャと比較しました（図4参照）。4つのニューラルネットワークが作成されました。AlphaGo Leeで使用されていたポリシーと値のネットワークが別々に使用されているもの、またはAlphaGo Zeroで使用されていたポリシーと値のネットワークを組み合わせたもの、そしてAlphaGo Leeの畳み込みネットワークアーキテクチャまたはAlphaGo Zeroの残差ネットワークアーキテクチャのいずれかが使用されていました。各ネットワークは、72時間のセルフプレイトレーニング後にAlphaGo Zeroによって生成されたセルフプレイゲームの固定データセットを使用して、同じ損失関数（式（1））を最小化するようにトレーニングされました。残差ネットワークの使用により、より正確で、エラーが少なくなり、AlphaGoのパフォーマンスが600 Elo以上向上しました。ポリシーと値を単一のネットワークに統合すると、着手の予測精度はわずかに低下しましたが、値のエラーが減少し、AlphaGoのプレイパフォーマンスがさらに約600 Elo向上しました。これは計算効率の向上によるところが大きいですが、より重要なのは、二重目的関数によってネットワークが複数のユースケースをサポートする共通表現に正規化されることです。

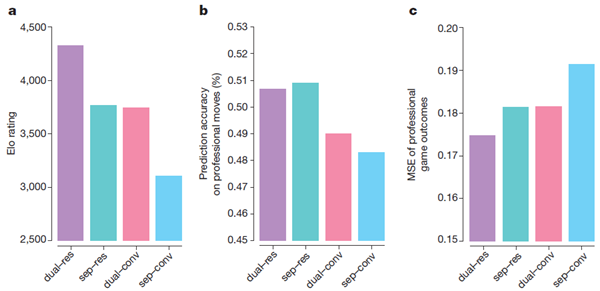
図4 | AlphaGo ZeroとAlphaGo Leeのニューラルネットワークアーキテクチャの比較 個別（sep）ネットワークまたはポリシーと値を組み合わせた（dual）ネットワーク、そして畳み込み（conv）ネットワークまたは残差（res）ネットワークを使用したニューラルネットワークアーキテクチャの比較。「dual-res」と「sep-conv」の組み合わせは、それぞれAlphaGo ZeroとAlphaGo Leeで使用されているニューラルネットワークアーキテクチャに対応しています。各ネットワークは、AlphaGo Zeroの以前の実行によって生成された固定データセットで学習されました。a 学習済みの各ネットワークは、異なるプレイヤーを取得するためにAlphaGo Zeroの探索と組み合わせられました。Eloレーティングは、これらの異なるプレイヤー間の評価ゲームから、1手あたり5秒の思考時間を使用して計算されました。b 各ネットワークアーキテクチャにおける、人間のプロの手に対する予測精度（GoKifuデータセットより）。 c 各ネットワークアーキテクチャにおける、人間のプロのゲーム結果（GoKifuデータセットより）のMSE。

AlphaGo Zero が学習した知識

AlphaGo Zero は、自己対局の学習プロセス中に、驚くべきレベルの囲碁の知識を発見しました。これには、人間の囲碁の基本的な知識だけでなく、従来の囲碁の知識の範囲を超えた非標準的な戦略も含まれていました。

図5は、プロの定石（コーナーシーケンス）が発見された時期を示すタイムラインを示しています（図5aおよび拡張データ図2）。最終的に、AlphaGo Zeroは、これまで知られていなかった新しい定石のバリエーションを好みました（図5bおよび拡張データ図3）。図5cは、トレーニングのさまざまな段階で行われたいくつかの高速セルフプレイゲームを示しています（補足情報を参照）。トレーニング中に定期的に行われたトーナメントの長さのゲームは、拡張データ図4および補足情報に示されています。AlphaGo Zeroは、完全にランダムな手から、布石（オープニング）、手筋（戦術）、死活、コウ（繰り返しの盤面状況）、寄せ（エンドゲーム）、競争の獲得、先手（イニシアチブ）、形、影響力、領土など、囲碁の概念を基礎から発見し、高度な理解へと急速に進歩しました。驚くべきことに、人間が最初に習得した囲碁の知識の要素の一つである「しちょう」（盤全体にまたがることもある「梯子」状の捕捉手順）は、AlphaGo Zero がトレーニングのずっと後になって初めて理解したものでした。

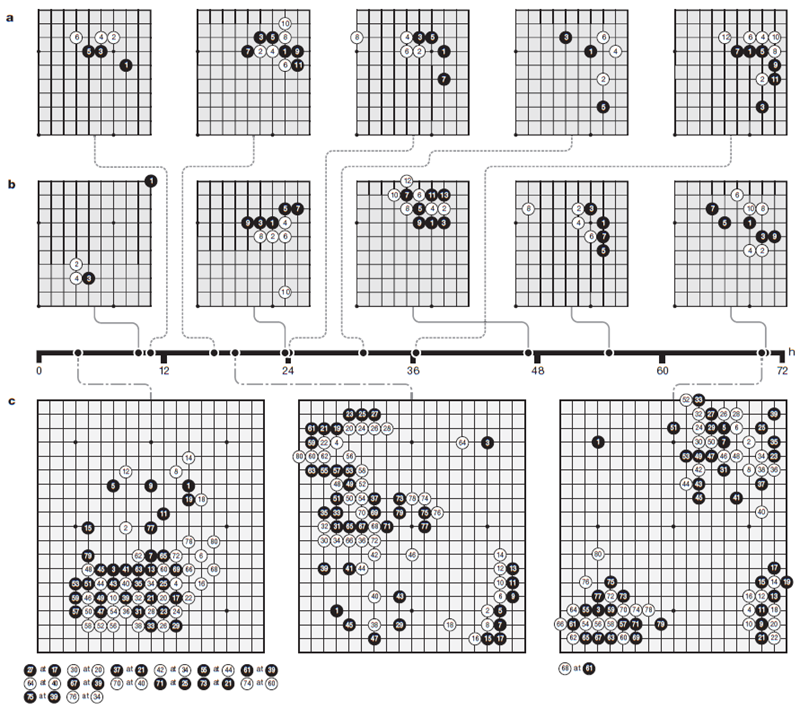
図5 | AlphaGo Zeroが学習した囲碁の知識。a AlphaGo Zeroのトレーニング中に発見された5つの人間の定石（一般的な角の並び）。関連するタイムスタンプは、自己対局トレーニング中に各並びが最初に発生した時刻（回転と反射を考慮）を示しています。拡張データ図2は、各並びのトレーニング中の出現頻度を示しています。b 自己対局トレーニングのさまざまな段階で好まれた5つの定石。表示されている各角の並びは、自己対局トレーニングの反復中に、すべての角の並びの中で最も頻繁にプレイされました。その反復のタイムスタンプはタイムラインに示されています。10時間後には、弱い角の手が好まれました。47時間後には、3-3の侵入が最も頻繁にプレイされました。この定石は人間のプロ対局でも一般的ですが、AlphaGo Zeroは後に新しい変化を発見し、好むようになりました。拡張データ図3は、5つのすべての並びと新しい変化の経時的な出現頻度を示しています。 c 訓練段階の異なる3つのセルフプレイゲームの最初の80手。1回の探索あたり1,600回のシミュレーション（約0.4秒）を用いて行われた。3時間では、ゲームは人間の初心者のように貪欲に石を取ることに焦点を当てている。19時間では、ゲームは生死、影響力、領土の基本を示している。70時間では、ゲームは驚くほどバランスが取れており、複数の戦闘と複雑なコウの戦いを経て、最終的に白の半点勝利に終わった。完全なゲームについては補足情報を参照。

AlphaGo Zero の最終パフォーマンス

その後、より大規模なニューラルネットワークとより長い期間を用いて、2つ目のAlphaGo Zeroインスタンスに強化学習パイプラインを適用しました。トレーニングは再び完全にランダムな動作から開始し、約40日間継続しました。

訓練期間中、2,900万回の自己対戦ゲームが生成されました。パラメータは、それぞれ2,048個のポジションからなる310万回のミニバッチから更新されました。ニューラルネットワークには40個の残差ブロックが含まれていました。学習曲線は図6aに示されています。訓練期間中、一定の間隔で行われたゲームは、拡張データ図5と補足情報に示されています。

我々は、完全に学習済みのAlphaGo Zeroを、AlphaGo Fan、AlphaGo Lee、そして過去のいくつかの囲碁プログラムとの内部トーナメントを用いて評価しました。また、現存する最強プログラムであるAlphaGo Masterとも対局を行いました。AlphaGo Masterは、本論文で紹介したアルゴリズムとアーキテクチャに基づき、人間のデータと特徴量を使用しています（方法の項を参照）。AlphaGo Masterは、2017年1月にオンライン対局で最強のプロ棋士を60対0で破りました34。評価では、すべてのプログラムに1手あたり5秒の思考時間を与えました。AlphaGo ZeroとAlphaGo Masterはそれぞれ4つのTPUを搭載した単一のマシンで対戦しました。AlphaGo FanとAlphaGo Leeは、それぞれ176個のGPUと48個のTPUに分散配置されました。また、AlphaGo Zeroの生のニューラルネットワークのみに基づいたプレイヤーも含めました。このプレイヤーは、単に最大確率で手を選択しました。

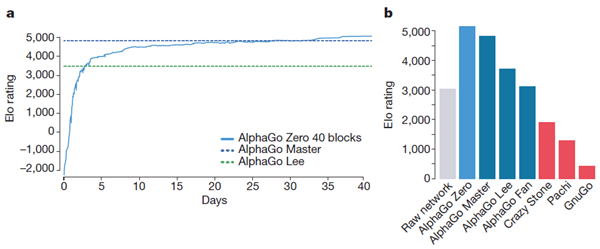
図6bは、各プログラムのEloスケールでのパフォーマンスを示しています。先読みを一切行っていない生のニューラルネットワークは、Eloレーティング3,055を達成しました。AlphaGo Zeroのレーティングは5,185で、AlphaGo Masterは4,858、AlphaGo Leeは3,739、AlphaGo Fanは3,144でした。

最後に、2時間の制限時間を設けた100局対局で、AlphaGo ZeroとAlphaGo Masterの直接対決を評価しました。AlphaGo Zeroは89対11で勝利しました（拡張データ図6および補足情報を参照）。

結論

我々の研究結果は、純粋な強化学習アプローチが最も困難な領域においても完全に実行可能であることを包括的に示しています。人間の例や指導なしに、基本的なルール以外の知識がなくても、超人的なレベルまで訓練することが可能です。さらに、純粋な強化学習アプローチは、人間の専門家のデータを用いた訓練と比較して、訓練にわずか数時間長くかかるだけで、はるかに優れた漸近的性能を達成します。このアプローチを用いることで、AlphaGo Zeroは、人間のデータと人為的に作成された特徴を用いて訓練された、これまでの最強バージョンのAlphaGoを、大きな差で打ち負かしました。

人類は数千年にわたり、数百万もの囲碁のゲームから知識を蓄積し、それらをパターン、ことわざ、書物へと凝縮してきました。AlphaGo Zeroは、わずか数日間で、白紙の状態からスタートし、囲碁に関する知識の多くを再発見するとともに、最古のゲームへの新たな洞察をもたらす斬新な戦略を発見しました。

(参考文献)

1. Friedman, J., Hastie, T. & Tibshirani, R. The Elements of Statistical Learning: Data Mining, Inference, and Prediction (Springer, 2009).

2. LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436–444 (2015).

3. Krizhevsky, A., Sutskever, I. & Hinton, G. ImageNet classification with deep convolutional neural networks. In Adv. Neural Inf. Process. Syst. Vol. 25 (eds Pereira, F., Burges, C. J. C., Bottou, L. & Weinberger, K. Q.) 1097–1105 (2012).

4. He, K., Zhang, X., Ren, S. & Sun, J. Deep residual learning for image recognition. In Proc. 29th IEEE Conf. Comput. Vis. Pattern Recognit. 770–778 (2016).

5. Hayes-Roth, F., Waterman, D. & Lenat, D. Building Expert Systems (Addison- Wesley, 1984).

6. Mnih, V. et al. Human-level control through deep reinforcement learning. Nature 518, 529–533 (2015).

7. Guo, X., Singh, S. P., Lee, H., Lewis, R. L. & Wang, X. Deep learning for real-time Atari game play using offline Monte-Carlo tree search planning. In Adv. Neural Inf. Process. Syst. Vol. 27 (eds Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N. D. & Weinberger, K. Q.) 3338–3346 (2014).

8. Mnih, V. et al. Asynchronous methods for deep reinforcement learning. In Proc. 33rd Int. Conf. Mach. Learn. Vol. 48 (eds Balcan, M. F. & Weinberger, K. Q.) 1928–1937 (2016).

9. Jaderberg, M. et al. Reinforcement learning with unsupervised auxiliary tasks. In 5th Int. Conf. Learn. Representations (2017).

10. Dosovitskiy, A. & Koltun, V. Learning to act by predicting the future. In 5th Int. Conf. Learn. Representations (2017).

11. Man´dziuk, J. in Challenges for Computational Intelligence (Duch, W. & Man´dziuk, J.) 407–442 (Springer, 2007).

12. Silver, D. et al. Mastering the game of Go with deep neural networks and tree search. Nature 529, 484–489 (2016).

13. Coulom, R. Efficient selectivity and backup operators in Monte-Carlo tree search. In 5th Int. Conf. Computers and Games (eds Ciancarini, P. & van den Herik, H. J.) 72–83 (2006).

14. Kocsis, L. & Szepesvári, C. Bandit based Monte-Carlo planning. In 15th Eu. Conf. Mach. Learn. 282–293 (2006).

15. Browne, C. et al. A survey of Monte Carlo tree search methods. IEEE Trans. Comput. Intell. AI Games 4, 1–49 (2012).

16. Fukushima, K. Neocognitron: a self organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biol. Cybern. 36, 193–202 (1980).

17. LeCun, Y. & Bengio, Y. in The Handbook of Brain Theory and Neural Networks Ch. 3 (ed. Arbib, M.) 276–278 (MIT Press, 1995).

18. Ioffe, S. & Szegedy, C. Batch normalization: accelerating deep network training by reducing internal covariate shift. In Proc. 32nd Int. Conf. Mach. Learn. Vol. 37 448–456 (2015).

19. Hahnloser, R. H. R., Sarpeshkar, R., Mahowald, M. A., Douglas, R. J. & Seung, H. S. Digital selection and analogue amplification coexist in a cortex-inspired silicon circuit. Nature 405, 947–951 (2000).

20. Howard, R. Dynamic Programming and Markov Processes (MIT Press, 1960).

21. Sutton, R. & Barto, A. Reinforcement Learning: an Introduction (MIT Press, 1998).

22. Bertsekas, D. P. Approximate policy iteration: a survey and some new methods. J. Control Theory Appl. 9, 310–335 (2011).

23. Scherrer, B. Approximate policy iteration schemes: a comparison. In Proc. 31st Int. Conf. Mach. Learn. Vol. 32 1314–1322 (2014).

24. Rosin, C. D. Multi-armed bandits with episode context. Ann. Math. Artif. Intell. 61, 203–230 (2011).

25. Coulom, R. Whole-history rating: a Bayesian rating system for players of time-varying strength. In Int. Conf. Comput. Games (eds van den Herik, H. J., Xu, X. Ma, Z. & Winands, M. H. M.) Vol. 5131 113–124 (Springer, 2008).

26. Laurent, G. J., Matignon, L. & Le Fort-Piat, N. The world of independent learners is not Markovian. Int. J. Knowledge-Based Intelligent Engineering Systems 15, 55–64 (2011).

27. Foerster, J. N. et al. Stabilising experience replay for deep multi-agent reinforcement learning. In Proc. 34th Int. Conf. Mach. Learn. Vol. 70 1146–1155 (2017).

28. Heinrich, J. & Silver, D. Deep reinforcement learning from self-play in imperfect-information games. In NIPS Deep Reinforcement Learning Workshop (2016).

29. Jouppi, N. P. et al. In-datacenter performance analysis of a Tensor Processing Unit. Proc. 44th Annu. Int. Symp. Comp. Architecture Vol. 17 1–12 (2017).

30. Maddison, C. J., Huang, A., Sutskever, I. & Silver, D. Move evaluation in Go using deep convolutional neural networks. In 3rd Int. Conf. Learn. Representations. (2015).

31. Clark, C. & Storkey, A. J. Training deep convolutional neural networks to play Go. In Proc. 32nd Int. Conf. Mach. Learn. Vol. 37 1766–1774 (2015).

32. Tian, Y. & Zhu, Y. Better computer Go player with neural network and long-term prediction. In 4th Int. Conf. Learn. Representations (2016).

33. Cazenave, T. Residual networks for computer Go. IEEE Trans. Comput. Intell. AI Games https://doi.org/10.1109/TCIAIG.2017.2681042 (2017).

34. Huang, A. AlphaGo master online series of games. https://deepmind.com/ research/AlphaGo/match-archive/master (2017).

謝辞

図表作成にご協力いただいたA. Cain氏、論文査読にご協力いただいたA. Barreto氏、G. Ostrovski氏、T. Ewalds氏、T. Schoul氏、J. Oh氏、N. Heess氏、そしてDeepMindチームの皆様のご支援に感謝申し上げます。

方法

強化学習
方策反復^20,21は、方策評価（現在の方策の価値関数を推定する）と方策改善（現在の価値関数を用いてより良い方策を生成する）を交互に行うことで、改善する方策のシーケンスを生成する古典的なアルゴリズムです。方策評価への単純なアプローチは、サンプリングされた軌跡の結果から価値関数を推定することです^35,36。方策改善への単純なアプローチは、価値関数に関して貪欲に行動を選択することです²⁰。大きな状態空間では、各方策を評価し、その改善を表すために近似値が必要です^22,23。

分類ベースの強化学習³⁷は、単純なモンテカルロ探索を用いて方策を改善する。各行動に対して多数のロールアウトが実行され、平均値が最大となる行動が正の訓練例となり、それ以外の行動は負の訓練例となる。その後、行動を正または負に分類するように方策が訓練され、後続のロールアウトで使用される。これは、\(τ→ 0\) の場合のAlphaGo Zeroの訓練アルゴリズムの方策コンポーネントの前身と見なすことができる。

より最近の例として、分類ベースの修正ポリシー反復（CBMPI: Classification-based modified policy iteration）が挙げられます。CBMPIは、AlphaGo Zeroの価値要素と同様に、価値関数を切り捨てロールアウト値に回帰させることでポリシー評価を実行します。この手法は、テトリスのゲームにおいて最先端の結果を達成しました38。しかし、この先行研究は、単純なロールアウトと、手作業で作成された特徴量を用いた線形関数近似に限られていました。

AlphaGo Zeroのセルフプレイアルゴリズムも同様に、MCTSをポリシー改善とポリシー評価の両方に用いる近似ポリシー反復スキームとして理解できる。ポリシー改善はニューラルネットワークポリシーから始まり、そのポリシーの推奨に基づいてMCTSを実行し、（より強力な）探索ポリシーをニューラルネットワークの関数空間に投影し直す。ポリシー評価は（より強力な）探索ポリシーに適用され、セルフプレイゲームの結果もニューラルネットワークの関数空間に投影し直される。これらの投影ステップは、ニューラルネットワークパラメータを、それぞれ探索確率とセルフプレイゲームの結果に一致するように訓練することによって実現される。

Guo et al.⁷ もまた、MCTS の出力をニューラルネットワークに投影します。これは、価値ネットワークを探索値に回帰させるか、MCTS によって選択された行動を分類することによって行われます。このアプローチは、Atari ゲームをプレイするためのニューラルネットワークの学習に使用されました。しかし、MCTS は固定されており、方策反復は行われず、学習済みのネットワークは利用されませんでした。ゲームにおける自己対戦強化学習。私たちのアプローチは、完全情報ゼロサムゲームに最も直接的に適用できます。私たちは、以前の研究¹² で説明した交代マルコフゲームの形式主義に従いますが、価値または方策反復に基づくアルゴリズムは、この設定に自然に拡張できることに留意します³⁹。

自己対戦強化学習は、これまで囲碁に適用されてきました。NeuroGo^40,41は、連結性、陣地、そして目に関する囲碁の知識に基づいた洗練されたアーキテクチャを用いて、ニューラルネットワークによって価値関数を表現しました。このニューラルネットワークは、先行研究⁴³に基づき、時間差分学習⁴²によって学習され、自己対戦における陣地予測を実現しました。関連するアプローチであるRLGO⁴⁴は、特徴量の線形結合によって価値関数を表現し、3×3の石のパターンをすべて網羅的に列挙しました。RLGOは時間差分学習によって学習され、自己対戦における勝者を予測しました。NeuroGoとRLGOはどちらも、アマチュアレベルの弱いレベルのプレイを達成しました。

MCTSは、自己対戦強化学習⁴⁵の一種と見なすこともできます。探索木のノードには、探索中に遭遇した局面の価値関数が含まれており、これらの値が更新されて、自己対戦のシミュレーションゲームの勝者を予測します。MCTSプログラムは、これまでに囲碁でアマチュアレベルの実力を発揮してきました^46,47が、その際には相当の専門知識が用いられています。具体的には、ゲーム終了までシミュレーションを実行して局面を評価する、手作業で作成された特徴に基づく高速ロールアウトポリシー^13,48と、探索木内の動きを選択する、同じく手作業で作成された特徴に基づくツリーポリシー⁴⁷です。

セルフプレイ強化学習アプローチは、チェス^49–51、チェッカー⁵²、バックギャモン⁵³、オセロ⁵⁴、スクラブル⁵⁵、そして最近ではポーカー⁵⁶といった他のゲームにおいても高いレベルのパフォーマンスを達成しています。これらの例すべてにおいて、価値関数は、セルフプレイによって生成された学習データから、回帰^54–56または時間差分学習^49–53によって学習されました。学習された価値関数は、アルファベータ探索^49–54、単純モンテカルロ探索^55,57、または反事実的後悔最小化56における評価関数として使用されました。しかし、これらの手法では、手作業で作成された入力特徴^49–53,56 または手作業で作成された特徴テンプレート^54,55が使用されていました。さらに、学習プロセスでは、重みの初期化に教師あり学習が使用され⁵⁸、駒の価値に対する重みが手作業で選択され^49,51,52、行動空間に対する制約が手作業で作成され56、既存のコンピュータプログラムがトレーニング用の対戦相手として使用され^49,50、または棋譜が生成され⁵¹ていました。

最も成功し、広く使用されている強化学習手法の多くは、ゼロサムゲームの文脈で初めて導入されました。例えば、時間差分学習はチェッカーをプレイするプログラム59で初めて導入され、MCTSは囲碁で導入されました¹³。しかし、非常によく似たアルゴリズムがその後、ビデオゲーム^6–8,10、ロボット工学⁶⁰、産業制御^61–63、オンラインレコメンデーションシステム^64,65において非常に効果的であることが証明されました。

AlphaGo のバージョン
AlphaGo の3つの異なるバージョンを比較します。

(1) AlphaGo Fan は、2015年10月に樊慧と対戦した、以前に公開されたプログラム¹² です。このプログラムは、176台のGPUを使用して多数のマシンに分散されていました。

(2) AlphaGo Lee は、2016年3月に李世ドルを4対1で破ったプログラムです。これは以前は未公開でしたが、ほとんどの点で AlphaGo Fan12 に似ています。しかし、公平な比較を行うために、いくつかの重要な違いを強調します。まず、価値ネットワークは、ポリシーネットワークによる自己対戦のゲームではなく、AlphaGo による高速自己対戦のゲームの結果から学習されました。この手順は複数回反復されました。これは、本論文で提示するタブラ・ラサ・アルゴリズムへの最初のステップです。第二に、方策ネットワークと価値ネットワークは、元の論文で説明されたもの（256平面の畳み込み層を12層使用）よりも大規模であり、より多くの反復で学習されました。また、このプレイヤーはGPUではなく48個のTPUを使用して多数のマシンに分散されており、探索中にニューラルネットワークをより高速に評価することができました。

(3) AlphaGo Masterは、2017年1月にトッププレイヤーを60対0で破ったプログラムです34。これは未発表でしたが、本論文で説明されているものと同じニューラルネットワークアーキテクチャ、強化学習アルゴリズム、MCTSアルゴリズムを使用しています。ただし、AlphaGo Lee12と同じ手作業で作成された特徴量とロールアウトを使用しており、学習は人間のデータを用いた教師あり学習によって初期化されています。

(4) AlphaGo Zeroは、本論文で説明されているプログラムです。 AlphaGo Zeroは、ランダムな初期重みから開始し、ロールアウトや人間の監督なしに、生の盤面履歴のみを入力特徴として用いるセルフプレイ強化学習によって学習します。Google Cloud内の4つのTPUを搭載したマシン1台のみを使用します（AlphaGo Zeroは分散配置も可能ですが、可能な限りシンプルな探索アルゴリズムを使用することにしました）。

ドメイン知識
私たちの主な貢献は、人間のドメイン知識がなくても超人的なパフォーマンスを達成できることを実証することです。この貢献を明確にするために、AlphaGo Zeroがトレーニング手順またはMCTSにおいて明示的または暗黙的に使用するドメイン知識を列挙します。これらは、AlphaGo Zeroが異なる（交代マルコフ）ゲームを学習するために置き換える必要がある知識項目です。

(1) AlphaGo Zeroには、ゲームルールに関する完全な知識が提供されます。これらは、MCTS中に、一連の動きから生じる局面をシミュレートし、終了状態に到達したシミュレーションのスコアリングに使用されます。ゲームは、両方のプレイヤーがパスするか、19 × 19 × 2 = 722手後に終了します。さらに、プレイヤーには各局面における有効な動きのセットが提供されます。

(2) AlphaGo Zeroは、MCTSシミュレーションおよび自己対戦トレーニング中にTromp–Taylorスコアリング66を使用します。これは、人間のスコア（中国、日本、韓国のルール）は、領土の境界が解決される前にゲームが終了した場合、明確に定義されないためです。ただし、すべてのトーナメントおよび評価ゲームは中国のルールを使用してスコア付けされました。

(3) 局面を記述する入力特徴は19×19の画像として構造化されています。つまり、ニューラルネットワークのアーキテクチャは盤のグリッド構造と一致しています。

(4) 囲碁のルールは回転と反射に対して不変です。この知識は、AlphaGo Zeroで、トレーニング中にデータセットを拡張して各局面の回転と反射を含めることと、MCTS中に局面のランダムな回転または反射をサンプリングすることの両方によって活用されています（探索アルゴリズムを参照）。コミ以外にも、囲碁のルールは色の転置に対して不変です。この知識は、現在のプレイヤーの視点から盤を表現することで活用されています（ニューラルネットワークアーキテクチャを参照）。

AlphaGo Zeroは、上記に挙げた点以外、いかなるドメイン知識も使用しません。ディープニューラルネットワークは、葉ノードの評価と着手の選択にのみ使用します（「探索アルゴリズム」参照）。ロールアウトポリシーやツリーポリシーは使用せず、MCTSは他のヒューリスティックやドメイン固有のルールによって拡張されていません。有効な着手は排除されません。たとえ対局者の目が塞がっている着手であってもです（これは、これまでのすべてのプログラムで使用されている標準的なヒューリスティックです⁶⁷）。

アルゴリズムは、ニューラルネットワークの初期パラメータをランダムに設定して開始されました。ニューラルネットワークのアーキテクチャ（「ニューラルネットワークのアーキテクチャ」を参照）は、画像認識における最新の技術4,18に基づいており、トレーニング用のハイパーパラメータはそれに応じて選択されました（「セルフプレイトレーニングパイプライン」を参照）。MCTS探索パラメータは、予備実行で学習されたニューラルネットワークを用いてAlphaGo Zeroのセルフプレイ性能を最適化するために、ガウス過程最適化68によって選択されました。より大規模な実行（40ブロック、40日間）では、より小規模な実行（20ブロック、3日間）で学習されたニューラルネットワークを用いてMCTS探索パラメータが再最適化されました。トレーニングアルゴリズムは、人間の介入なしに自律的に実行されました。

セルフプレイ学習パイプライン
AlphaGo Zero のセルフプレイ学習パイプラインは、3 つの主要コンポーネントで構成され、すべて非同期かつ並列に実行されます。ニューラルネットワークパラメータ \(θ_i\) は、最新のセルフプレイデータから継続的に最適化され、AlphaGo Zero のプレイヤー \(α_{θ_i}\) は継続的に評価され、これまでの最高のパフォーマンスを示すプレイヤー \(α_{θ_∗}\) が、新しいセルフプレイデータの生成に使用されます。

最適化
各ニューラルネットワーク \(f_{θ_i}\) は、Google Cloud 上で TensorFlow を使用して最適化され、64 台の GPU ワーカーと 19 台の CPU パラメータサーバーが稼働しています。バッチサイズはワーカーあたり 32 で、合計ミニバッチサイズは 2,048 です。各ミニバッチのデータは、最新の 500,000 回のセルフプレイの全ポジションから均一にランダムにサンプリングされます。ニューラルネットワークのパラメータは、式 (1) の損失を用いて、モメンタム法と学習率アニーリング法を用いた確率的勾配降下法によって最適化されます。学習率は、拡張データ表 3 の標準スケジュールに従ってアニーリングされます。モメンタムパラメータは 0.9 に設定されています。クロスエントロピー損失とMSE損失は均等に重み付けされ（報酬は単位スケール、\(r ∈ \{-1, +1\}\) であるため、これは妥当です）、L2正則化パラメータは \(c = 10^{−4}\) に設定されます。最適化プロセスは、1,000回の訓練ステップごとに新しいチェックポイントを生成します。このチェックポイントは評価器によって評価され、次に説明するように、次の一連のセルフプレイゲームを生成するために使用される場合があります。

評価器
常に最高品質のデータを生成するために、データ生成に使用する前に、新しいニューラルネットワークのチェックポイントを現在の最良ネットワーク \(f_{θ_∗}\) と比較します。ニューラルネットワーク \(f_{θ_i}\) は、\(f_{θ_i}\) を使用して葉の位置と事前確率を評価する MCTS 検索 \(α_{θ_i}\) のパフォーマンスによって評価されます（検索アルゴリズムを参照）。各評価は 400 回のゲームで構成され、MCTS を使用して 1,600 回のシミュレーションで各手を選択し、微小温度 \(τ→ 0\) を使用します（つまり、最も強いプレイを提供するために、訪問回数が最大となる手を決定論的に選択します）。新しいプレイヤーが 55% を超える差で勝った場合（ノイズのみに基づいて選択することを避けるため）、そのプレイヤーは最良プレイヤー \(α_{θ_∗}\) となり、その後、自己プレイ生成に使用され、また、後続の比較の基準にもなります。

自己対局
評価者によって選択された、現在最も優れたプレイヤー αθ∗ を用いてデータを生成します。各反復において、\(α_{θ_∗}\) は 25,000 回の自己対局を行い、各手を選択するために 1,600 回の MCTS シミュレーションを使用します（これには 1 回の探索あたり約 0.4 秒かかります）。各ゲームの最初の 30 手については、温度は \(τ = 1\) に設定されます。これにより、MCTS における移動回数に比例して手が選択され、多様な局面に遭遇することが保証されます。ゲームの残りの部分では、無限小温度、\(τ→ 0\) が使用されます。追加の探索は、ルートノード s0 の事前確率にディリクレノイズを追加することで実現されます。具体的には、\(P(s, a) = (1 − ε)p_a + εη_a\) です。ここで、\(\mathbf η ∼ Dir(0.03)\) かつ \(ε = 0.25\) です。このノイズにより、すべての手を試すことができますが、探索によって悪い手が却下される可能性があります。計算時間を節約するために、明らかに負けているゲームは投了されます。投了しきい値 vresign は、偽陽性（AlphaGo が投了していなければ勝てたはずのゲーム）の割合を 5% 未満に保つように自動的に選択されます。偽陽性を測定するために、自己対戦ゲームの 10% で投了を無効にして、終了までプレイします。

教師あり学習
比較のため、ニューラルネットワークパラメータ(θ_{SL}\)も教師あり学習によって学習させました。ニューラルネットワークのアーキテクチャはAlphaGo Zeroと同一です。KGSデータセットからデータ\((s, \mathbf π, z)\)のミニバッチをランダムにサンプリングし、人間の熟練者の手aを\(π_a = 1\)に設定しました。パラメータは、モメンタム法と学習率アニーリング法を用いた確率的勾配降下法によって最適化されました。損失は式(1)と同じですが、MSE成分に0.01の重み付けをしました。学習率は、拡張データ表3の標準スケジュールに従ってアニーリングされました。モメンタムパラメータは0.9、L2正則化パラメータは\(c = 10^{-4}\)に設定されました。

方策と価値ネットワークを組み合わせたアーキテクチャを使用し、価値コンポーネントの重みを低くすることで、価値への過剰適合（前研究¹²で報告された問題）を回避することができました。72時間後、着手予測精度は前研究^12,30–33で報告された最先端技術を上回り、KGSテストセットで60.4%に達しました。価値予測誤差も、前研究¹²よりも大幅に改善されました。検証セットは、囲碁棋譜のプロの対局で構成されました。精度とMSEは、それぞれ拡張データ表1と拡張データ表2に報告されています。

探索アルゴリズム
AlphaGo Zero は、AlphaGo Fan と AlphaGo Lee で使用されている非同期ポリシー・値 MCTS アルゴリズム (APV-MCTS) の、よりシンプルな派生版を使用しています。

探索木の各ノードsには、すべての法的アクション\(a∈A(s)\)に対するエッジ\((s, a)\)が含まれます。各エッジには統計量のセットが格納されます。 \[ \{N(s,a),W(s,a),Q(s,a),P(s,a)\} \] ここで、\(N(s, a)\) は訪問回数、\(W(s, a)\) は合計アクション値、\(Q(s, a)\) は平均アクション値、\(P(s, a)\) はそのエッジを選択する事前確率です。複数のシミュレーションは別々の探索スレッドで並列に実行されます。アルゴリズムは3つのフェーズ（図2a～c）を反復して進行し、次にプレイする手を選択します（図2d）。

選択（図2a）
選択フェーズはAlphaGo Fan¹²とほぼ同じです。ここでは完全性のために要約します。各シミュレーションの最初の木内フェーズは、探索木の根ノード \(s_0\) から始まり、タイムステップ \(L\) で葉ノード \(s_L\) に到達したときに終了します。これらのタイムステップ \(t < L\) において、探索木内の統計値 \(a_t =\underset{a}{argmax}(Q(s_t , a)+U(s_t , a))\) に基づいて、PUCTアルゴリズム²⁴の変種を用いてアクションが選択されます。 \[ U(s,a)=c_{puct}P(s,a)\frac{\sqrt{\sum_b N(s,b)}}{1+N(s,a)} \] ここで、\(c_{puct}\) は探索レベルを決定する定数です。この探索制御戦略は、最初は事前確率が高く訪問回数が少ない行動を優先しますが、漸近的には行動価値の高い行動を優先します。

展開して評価します (図 2b)。
リーフノード sL は、ニューラルネットワークの評価キューに追加されます。\((d_i(\mathbf p), v) = f_θ(d_i(s_L))\)。ここで、\(d_i\) は、[1..8] の範囲内の \(i\) から一様ランダムに選択された二面角反射または回転です。キュー内の位置は、ニューラルネットワークによって 8 のミニバッチサイズを使用して評価されます。評価が完了するまで、検索スレッドはロックされます。リーフノードが展開され、各エッジ \((s_L, a)\) は次のように初期化されます。\(\{N(s_L, a) = 0, W(s_L, a) = 0, Q(s_L, a) = 0, P(s_L, a) = p_a\}\);次に値 v がバックアップされます。

バックアップ（図2c）
エッジ統計は、各ステップ（t ≤ L）を逆方向にパスして更新されます。訪問回数は増加し（N(s_t, a_t) = N(s_t, a_t) + 1）、アクション値は平均値に更新されます（W(s_t, a_t) = W(s_t, a_t) + v,Q(s_t, a_t) = \frac{ W(s_t, a_t)}{N(s_t, a_t)}\) 各スレッドが異なるノードを評価することを保証するために、仮想損失を使用します ^12,69。

プレイ（図2d）
探索の終了時に、AlphaGo Zeroはルートポジションs0で、その指数化された訪問回数に比例する手aを選択します。\(π(a|s_0)=N(s_0, a)-{1/τ}/Σ_bN(s_0, b)^{1/τ}\)、ここで\(τ\)は探索レベルを制御する温度パラメータです。探索木は後続のタイムステップで再利用されます。つまり、プレイされたアクションに対応する子ノードが新しいルートノードになります。この子ノードの下のサブツリーは、そのすべての統計情報とともに保持され、ツリーの残りの部分は破棄されます。AlphaGo Zeroは、ルート値と最良の子ノード値が閾値\(v_{resign}\)よりも低い場合、投了します。

AlphaGo FanとAlphaGo LeeのMCTSと比較した主な違いは、AlphaGo Zeroはロールアウトを一切使用しないこと、別々のポリシーネットワークとバリューネットワークではなく単一のニューラルネットワークを使用すること、リーフノードは動的拡張ではなく常に拡張されること、各探索スレッドは評価とバックアップを非同期的に実行するのではなく、ニューラルネットワークの評価を単に待機すること、そしてツリーポリシーが存在しないことです。AlphaGo Zeroの大規模インスタンス（40ブロック、40日間）では、転置テーブルも使用されました。

ニューラルネットワークのアーキテクチャ
ニューラルネットワークへの入力は、17個の2値特徴平面で構成される19 × 19 × 17の画像スタックです。8つの特徴平面 (\(X_t\)) は、現在のプレイヤーの石の存在を示す2値で構成されます。((X_t^i=1\) は、時間ステップ (\(t\)) において、交差点 i にプレイヤーの色の石が含まれている場合、交差点が空であるか、相手の石が含まれているか、または (\(t < 0\)) の場合は0です。さらに8つの特徴平面 (\(Y_t\)) は、相手の石に対応する特徴を表します。最後の特徴平面 (C) は、打つべき色を表し、黒が打つ場合は1、白が打つ場合は0の定数値を持ちます。これらの平面は連結されて入力特徴 \(s_t = [X_t, Y_t, X_{t−1}, Y_{t−1},..., X_{t−7}, Y_{t−7}, C]\) を生成します。繰り返しが禁止されているため、囲碁は現在の石のみから完全には観察できないため、履歴特徴 \(X_t, Y_t\) は必要です。同様に、コミは観察できないため、色特徴 C も必要です。

入力特徴量stは、1つの畳み込みブロックとそれに続く19個または39個の残差ブロック⁴で構成される残差タワーによって処理されます。

各残差ブロックは、入力に対して以下のモジュールを順次適用します。

残差タワーの出力は、方策と値を計算するために2つの別々の「ヘッド」に渡されます。方策ヘッドは以下のモジュールを適用します。

すべての交差点とパスムーブのロジット確率に対応する。値ヘッドは以下のモジュールを適用する。

20ブロックまたは40ブロックのネットワークにおける全体的なネットワーク深度は、残差タワーの場合はそれぞれ39層または79層のパラメータ化層で、これにポリシーヘッドの場合は2層、バリューヘッドの場合は3層が加わります。

残差ネットワークの異なる変種が同時にコンピュータ囲碁³³に適用され、アマチュア段位レベルのパフォーマンスを達成したことに注目してください。ただし、これは教師あり学習のみで学習された単頭ポリシーネットワークに限定されていました。

ニューラルネットワークアーキテクチャの比較
図4は、ネットワークアーキテクチャの比較結果を示しています。具体的には、4つの異なるニューラルネットワークを比較しました。

(1) Dual-Res: ネットワークは、前述のように20ブロックの残差タワーを含み、その後にポリシーヘッドと値ヘッドが続きます。これはAlphaGo Zeroで使用されているアーキテクチャです。

(2) Sep-Res: ネットワークは20ブロックの残差タワーを2つ含みます。最初のタワーの後にはポリシーヘッドが、2番目のタワーの後には値ヘッドが続きます。

(3) Dual-Conv: ネットワークは12個の畳み込みブロックからなる非残差タワーを含み、その後にポリシーヘッドと値ヘッドが続きます。

(4) Sep-Conv: ネットワークは12個の畳み込みブロックからなる非残差タワーを2つ含みます。最初のタワーの後にはポリシーヘッドが、2番目のタワーの後には値ヘッドが続きます。これはAlphaGo Leeで使用されているアーキテクチャです。各ネットワークは、AlphaGo Zeroの前回実行で生成された最終200万局の自己対戦データを含む固定データセットを用いて、教師あり学習実験で説明したアニーリング率、モメンタム、正則化ハイパーパラメータを用いた確率的勾配降下法を用いて学習されました。ただし、利用可能なデータが多かったため、クロスエントロピーとMSEコンポーネントには均等に重み付けが行われました。

評価
AlphaGo Zero の相対的な強さ（図3a、6）を、各プレイヤーのEloレーティングを測定することで評価しました。プレイヤーaがプレイヤーbに勝つ確率をロジスティック関数 \(P(a\,defeats\,b)=\frac{1}{1+exp(c_{elo}(e(b)-e(a)}\) を用いて推定し、ベイズロジスティック回帰分析によってレーティング \(e(·)\) を推定しました。このレーティングは、BayesElo プログラム²⁵ を用いて、標準定数 \(c_{elo} = 1/400\) を用いて計算しました。

Eloレーティングは、AlphaGo Zero、AlphaGo Master、AlphaGo Lee、AlphaGo Fanによる1手5秒のトーナメント結果から計算されました。トーナメントには、AlphaGo Zeroの生のニューラルネットワークも使用されました。AlphaGo Fan、Crazy Stone、Pachi、GnuGoのEloレーティングは、以前の研究¹²のトーナメント値にアンカーされており、その研究で報告されたプレイヤーに対応しています。AlphaGo Fan対Fan Hui戦とAlphaGo Lee対Lee Sedol戦の結果も、スケールを人間の基準に合わせるために使用されました。そうしないと、AlphaGoのEloレーティングは、自己プレーバイアスにより非現実的に高くなります。

図3a、4a、6aのEloレーティングは、プレイヤー\(α_{θ_i}\)の自己対戦トレーニング中の各反復間の評価ゲームの結果から計算された。さらに、以前に公表された値¹²に固定されたEloレーティングを持つベースラインプレイヤーに対しても評価が行われた。

2016年ソウルで李世ドルと対戦した際に使用されたのと同じプレイヤーと対戦条件を用いて、AlphaGo ZeroとAlphaGo Leeの直接対決、およびAlphaGo ZeroとAlphaGo Masterの40ブロックインスタンスのパフォーマンスを測定しました。各プレイヤーには2時間の思考時間と、1手あたり60秒の3つの秒読みが与えられました。すべての対局は中国式ルールで採点され、コミは7.5点でした。

データの入手可能性
検証とテストに使用したデータセットは、GoKifuデータセット（http://gokifu.com/ から入手可能）とKGSデータセット（https://u-go.net/gamerecords/ から入手可能）です。

(参考文献：つづき)

35. Barto, A. G. & Duff, M. Monte Carlo matrix inversion and reinforcement learning. Adv. Neural Inf. Process. Syst. 6, 687–694 (1994).

36. Singh, S. P. & Sutton, R. S. Reinforcement learning with replacing eligibility traces. Mach. Learn. 22, 123–158 (1996).

37. Lagoudakis, M. G. & Parr, R. Reinforcement learning as classification: leveraging modern classifiers. In Proc. 20th Int. Conf. Mach. Learn. 424–431 (2003).

38. Scherrer, B., Ghavamzadeh, M., Gabillon, V., Lesner, B. & Geist, M. Approximate modified policy iteration and its application to the game of Tetris. J. Mach. Learn. Res. 16, 1629–1676 (2015).

39. Littman, M. L. Markov games as a framework for multi-agent reinforcement learning. In Proc. 11th Int. Conf. Mach. Learn. 157–163 (1994).

40. Enzenberger, M. The integration of a priori knowledge into a Go playing neural network. http://www.cgl.ucsf.edu/go/Programs/neurogo-html/neurogo.html (1996).

41. Enzenberger, M. in Advances in Computer Games (eds Van Den Herik, H. J., Iida, H. & Heinz, E. A.) 97–108 (2003).

42. Sutton, R. Learning to predict by the method of temporal differences. Mach. Learn. 3, 9–44 (1988).

43. Schraudolph, N. N., Dayan, P. & Sejnowski, T. J. Temporal difference learning of position evaluation in the game of Go. Adv. Neural Inf. Process. Syst. 6, 817–824 (1994).

44. Silver, D., Sutton, R. & Müller, M. Temporal-difference search in computer Go. Mach. Learn. 87, 183–219 (2012).

45. Silver, D. Reinforcement Learning and Simulation-Based Search in Computer Go. PhD thesis, Univ. Alberta, Edmonton, Canada (2009).

46. Gelly, S. & Silver, D. Monte-Carlo tree search and rapid action value estimation in computer Go. Artif. Intell. 175, 1856–1875 (2011).

47. Coulom, R. Computing Elo ratings of move patterns in the game of Go. Int. Comput. Games Assoc. J. 30, 198–208 (2007).

48. Gelly, S., Wang, Y., Munos, R. & Teytaud, O. Modification of UCT with patterns in Monte-Carlo Go. Report No. 6062 (INRIA, 2006).

49. Baxter, J., Tridgell, A. & Weaver, L. Learning to play chess using temporal differences. Mach. Learn. 40, 243–263 (2000).

50. Veness, J., Silver, D., Blair, A. & Uther, W. Bootstrapping from game tree search. In Adv. Neural Inf. Process. Syst. 1937–1945 (2009).

51. Lai, M. Giraffe: Using Deep Reinforcement Learning to Play Chess. MSc thesis, Imperial College London (2015).

52. Schaeffer, J., Hlynka, M. & Jussila, V. Temporal difference learning applied to a high-performance game-playing program. In Proc. 17th Int. Jt Conf. Artif. Intell. Vol. 1 529–534 (2001).

53. Tesauro, G. TD-gammon, a self-teaching backgammon program, achieves master-level play. Neural Comput. 6, 215–219 (1994).

54. Buro, M. From simple features to sophisticated evaluation functions. In Proc. 1st Int. Conf. Comput. Games 126–145 (1999).

55. Sheppard, B. World-championship-caliber Scrabble. Artif. Intell. 134, 241–275 (2002).

56. Moravcˇík, M. et al. DeepStack: expert-level artificial intelligence in heads-up no-limit poker. Science 356, 508–513 (2017).

57. Tesauro, G & Galperin, G. On-line policy improvement using Monte-Carlo search. In Adv. Neural Inf. Process. Syst. 1068–1074 (1996).

58. Tesauro, G. Neurogammon: a neural-network backgammon program. In Proc. Int. Jt Conf. Neural Netw. Vol. 3, 33–39 (1990).

59. Samuel, A. L. Some studies in machine learning using the game of checkers II - recent progress. IBM J. Res. Develop. 11, 601–617 (1967).

60. Kober, J., Bagnell, J. A. & Peters, J. Reinforcement learning in robotics: a survey. Int. J. Robot. Res. 32, 1238–1274 (2013).

61. Zhang, W. & Dietterich, T. G. A reinforcement learning approach to job-shop scheduling. In Proc. 14th Int. Jt Conf. Artif. Intell. 1114–1120 (1995).

62. Cazenave, T., Balbo, F. & Pinson, S. Using a Monte-Carlo approach for bus regulation. In Int. IEEE Conf. Intell. Transport. Syst. 1–6 (2009).

63. Evans, R. & Gao, J. Deepmind AI reduces Google data centre cooling bill by 40%. https://deepmind.com/blog/deepmind-ai-reduces-google-data-centrecooling- bill-40/ (2016).

64. Abe, N. et al. Empirical comparison of various reinforcement learning strategies for sequential targeted marketing. In IEEE Int. Conf. Data Mining 3–10 (2002).

65. Silver, D., Newnham, L., Barker, D., Weller, S. & McFall, J. Concurrent reinforcement learning from customer interactions. In Proc. 30th Int. Conf. Mach. Learn. Vol. 28 924–932 (2013).

66. Tromp, J. Tromp–Taylor rules. http://tromp.github.io/go.html (1995).

67. Müller, M. Computer Go. Artif. Intell. 134, 145–179 (2002).

68. Shahriari, B., Swersky, K., Wang, Z., Adams, R. P. & de Freitas, N. Taking the human out of the loop: a review of Bayesian optimization. Proc. IEEE 104, 148–175 (2016).

69. Segal, R. B. On the scalability of parallel UCT. Comput. Games 6515, 36–47 (2011).

(拡張データ：図表)

拡張データ図1｜2時間制限を用いたAlphaGo Zero（20ブロック、3日間）対AlphaGo Leeのトーナメント対局。最初の20局の100手を表示。全対局は補足情報に掲載されている。

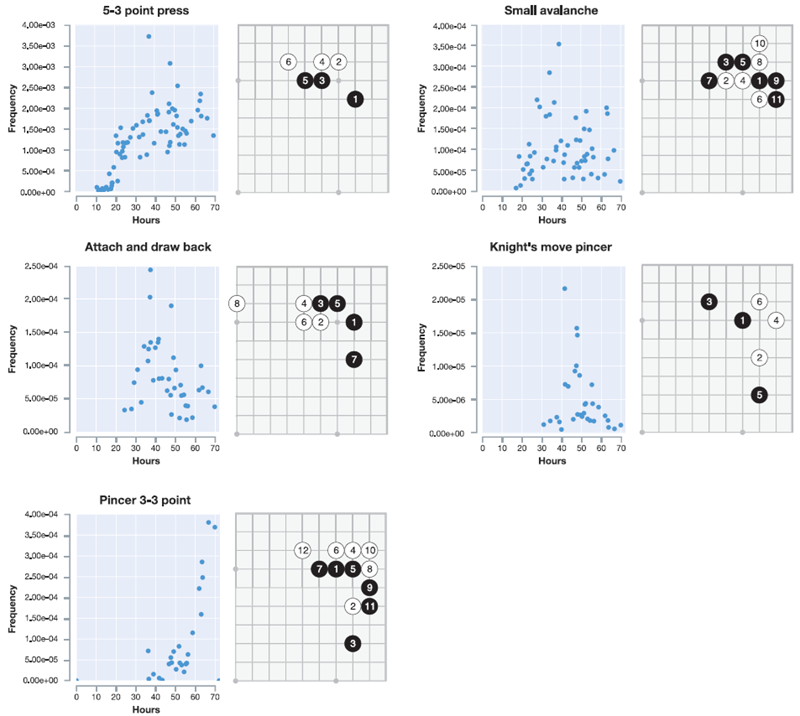
拡張データ図2 | 図5aの各定石（AlphaGo Zeroによって発見された、プロの対局でよく見られるコーナーシーケンス）のトレーニング中の出現頻度の経時変化。対応する定石は右側に表示されている。

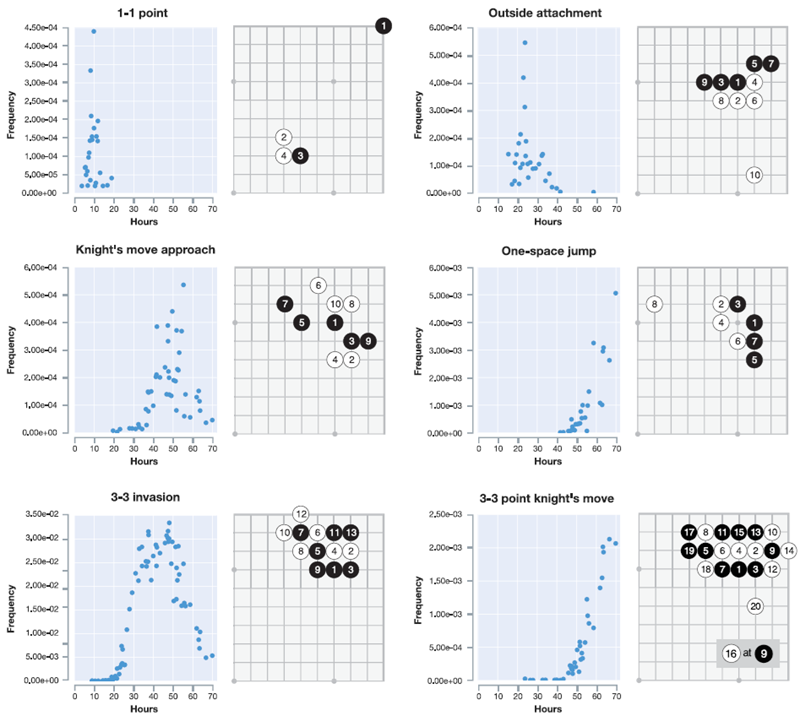
拡張データ図3 | 図5bの各定石（AlphaGo Zeroが少なくとも1回の反復で有利と判定したコーナーシーケンス）と追加のバリエーション1つについて、訓練中の時間経過に伴う出現頻度。対応する定石は右側に示されています。

拡張データ図4 | AlphaGo Zero（20ブロック）の自己対局。3日間のトレーニングランは20期間に分割されました。各期間の最強プレイヤー（評価者によって選出）が、2時間の制限時間を設け、自身と1対局を行いました。各対局には100手が表示されています。完全な対局は補足情報に記載されています。

拡張データ図5 | AlphaGo Zero（40ブロック）の自己対局。40日間のトレーニング期間は20期間に分割された。各期間の最高位プレイヤー（評価者によって選出）が、2時間の制限時間を設け、自身と1対局を行った。各対局には100手が示されており、完全な対局は補足情報に記載されている。

拡張データ図6 | AlphaGo Zero（40ブロック、40日間）とAlphaGo Masterトーナメントの2時間制対局。最初の20局の100手を表示。全局は補足情報に掲載。

拡張データ表 1 | 手予測精度
強化学習（AlphaGo Zero）または教師あり学習によって学習されたニューラルネットワークの手予測精度（パーセント）。教師あり学習では、ネットワークはKGSデータ（アマチュア対局）を用いて3日間学習されました。比較結果は参考文献12にも示されています。強化学習では、20ブロックのネットワークは3日間、40ブロックのネットワークは40日間学習されました。ネットワークは、GoKifuデータセットのプロの対局に基づく検証セットでも評価されました。

拡張データ表 2 | 対局結果予測誤差
強化学習（AlphaGo Zero）または教師あり学習によって学習されたニューラルネットワークの対局結果予測における平均二乗誤差。教師あり学習の場合、ネットワークはKGSデータ（アマチュア対局）を用いて3日間学習されました。比較結果は参考文献12にも示されています。強化学習の場合、20ブロックのネットワークは3日間、40ブロックのネットワークは40日間学習されました。ネットワークは、GoKifuデータセットのプロの対局に基づく検証セットでも評価されました。

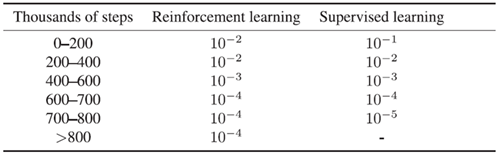
拡張データ表 3 | 学習率スケジュール
強化学習および教師あり学習の実験中に使用される学習率。ステップ数（ミニバッチ更新）で測定されます。

Mastering the game of Go without human knowledge

(要旨)